Smittespredning i samfundet
Undersiden “Smittespredning i samfundet” udgør sjette del af teorien for Biotech Academys materiale om Vacciner og COVID-19.
Mange sygdomme opfører sig nogenlunde ens, når det kommer til at smitte mennesker. Det er derfor, at vi vha. modeller kan forudsige, hvordan en sygdom kan sprede sig i et samfund, som f.eks. Danmark. En væsentlig information for at kunne bestemme dét er sygdommens reproduktionstal. Reproduktionstallet (også kendt som R0) for en sygdom beskriver, hvor mange raske personer én smittet person i gennemsnit smitter. Jo højere reproduktionstal, des mere smitsom er sygdommen. Er reproduktionstallet 3, betyder det, at en smittet person i gennemsnit når at smitte 3 personer, før vedkommende er rask igen.
Reproduktionstallet varierer fra sygdom til sygdom. Nogle sygdomme er altså mere smitsomme end andre. Her kan du se nogle forskellige eksempler på reproduktionstal for sygdomme:
| Sygdom |
Reproduktionstal, R0 |
| Mæslinger |
14 |
| SARS |
2 – 5 |
| Ebola |
1.5 – 2.5 |
| Influenza |
1.5 – 1.8 |
| COVID-19 |
1.4 – 3.9 |
Tabel 1. Reproduktionstallet på nogle udvalgte sygdomme.
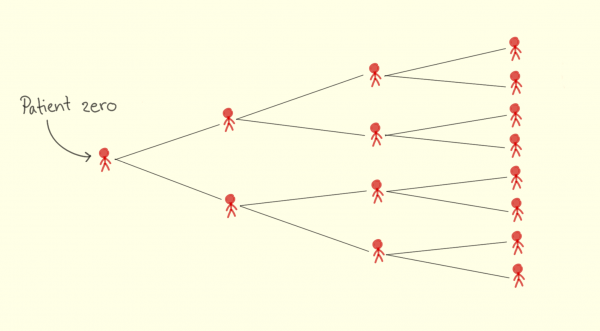
Nedenstående figur, viser en smittekæde på en sygdom med et reproduktionstal på 2.
Figur 2. Smitten spreder sig fra patient zero til resten af befolkningen. Røde personer er smittede. Figuren viser en sygdom med et reproduktionstal på 2.
Det er altså vigtigt at forstå, én smittet person hurtigt kan føre til rigtig mange smittede personer.
Med denne model kan vi undersøge, hvor lang tid der går, før der er 100 smittede, hvis vi bruger et reproduktionstal på 2. Vi siger, at en person smitter R0 (altså 2) personer dagen efter, at vedkommende selv er blevet smittet. I dette tankeeksperiment kan man altså kun smitte i én dag. Det er ikke sådan, det foregår i virkeligheden, hvor man kan smitte i flere dage.
Antagelsen om, at man kun smitter én dag, er god, når man skal udregne antallet af nye smittede over en periode. For at udregne, hvor mange nye smittede der er pr. dag, kan vi bruge nedenstående skema. Vi regner også det totale antal af smittede og ignorerer for en stund, at personer bliver raske.
| R0 = 2 |
Dag 0 |
Dag 1 |
Dag 2 |
Dag 3 |
Dag 4 |
Dag 5 |
Dag 6 |
Dag 7 |
| Regnestykket |
|
1 x 2 |
2 x 2 |
4 x 2 |
8 x 2 |
16 x 2 |
32 x 2 |
64 x 2 |
| Antal nye smittede |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
| Total antal smittede |
1 |
2 + 1 = 3 |
3 + 4 = 7 |
7 + 8 = 15 |
31 |
63 |
127 |
255 |
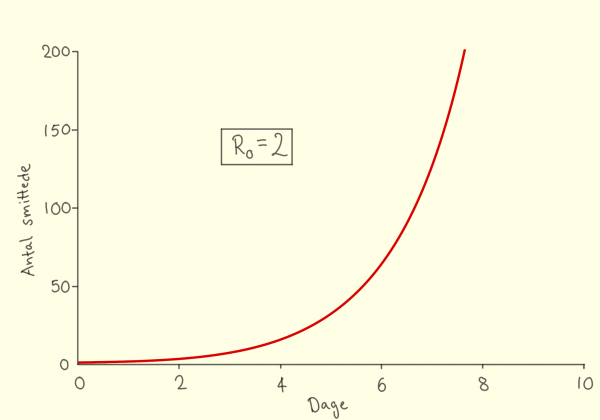
Figur 3. Grafen viser antal nye smittede pr. dag for en sygdom med reproduktionstallet 2.
I starten går smittespredningen langsomt, men pludselig begynder der at være rigtigt mange nye smittede. Denne form for udvikling kaldes eksponentiel udvikling, og den ses ofte i matematik, f.eks. når man skal regne på renter i en bank.
Prøv selv kræfter med beregninger af antallet af smittede i et samfund i opgaven: Regn på reproduktionstallet
Hvis reproduktionstallet er lavere end 1, hvad vil der så ske? Vi undersøger det på samme måde som ovenfor. Denne gang undersøger vi, hvad der sker, når vi har 8 smittede og har et reproduktionstal på 0.5.
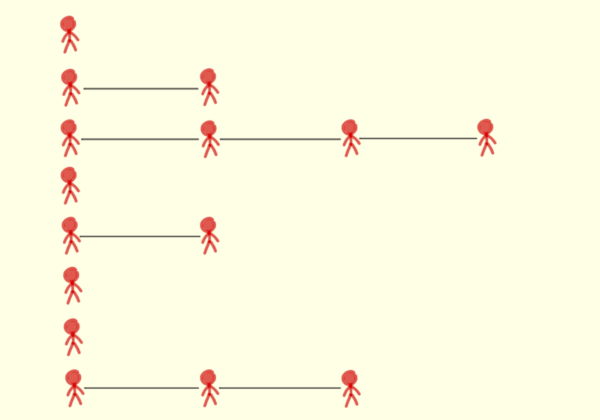
Hver person smitter kun en halv person i gennemsnit. Det er det samme som, at hver anden person giver smitten videre til 1 person, og hver anden person ikke giver smitten videre. Sygdommen spreder sig ikke mere – tværtimod! Med et reproduktionstal under 1, vil antallet af smittede falde, og til sidst vil sygdommen helt være forsvundet (se Figur 4).
Figur 4. Når reproduktionstallet er mindre end 1, vil antallet af nye smittede falde. Her ses smittekæder, hvor reproduktionstallet er 0.5.
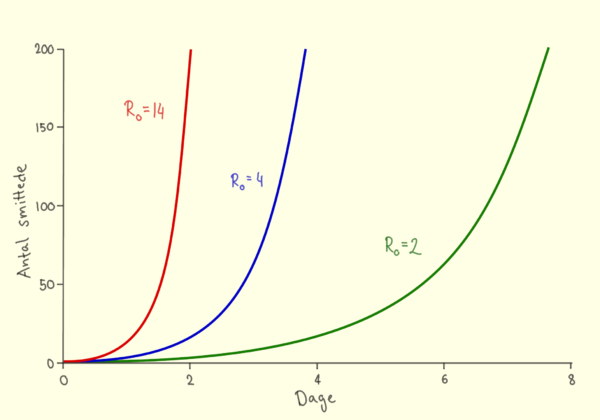
Herunder kan du se nogle grafer for forskellige værdier af R0.