Statistisk signifikans referer til, om et resultat skyldes tilfældigheder, eller om der ligger en særlig årsag bag. Når et resultat er statistisk signifikant, kan man føle sig ret sikker på, at de resultater man observerer, er rigtige og ikke bare er et held/uheld.
Når man laver forsøg, vil man ofte gerne sammenligne to eller flere forsøgsbetingelser. Det kan være, at man vil finde ud af, om folk er bedst til at fokusere før eller efter, de har drukket kaffe. Det kan også være, at man vil undersøge, om en bakterie vokser hurtigst ved 35, 37 eller 39 grader.
Når man analyserer sine forsøgsresultater, er det ofte relevant at sammenligne resultaterne ved de forskellige betingelser. Det er dog helt naturligt, at forsøgsresultater varierer lidt, hver gang man udfører forsøgene, også selvom man har gennemført forsøget ved samme betingelser. Det er derfor nødvendigt at have nogle redskaber til at finde ud af, om variationen bare er tilfældig eller rent faktisk skyldes de ændrede forsøgsbetingelser. Til det bruger man statistik.
Eksempel 1
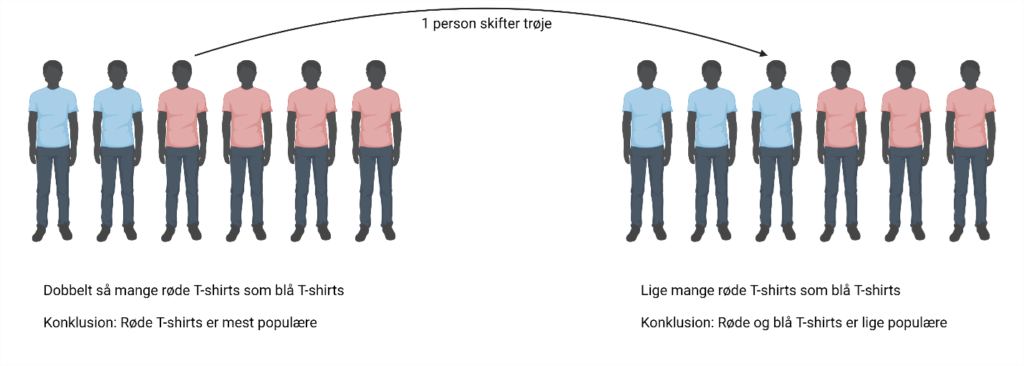
Lad os se på et eksempel. Du vil gerne undersøge, om din klasse går mest i røde eller blå T-shirts. Du vælger derfor at tælle, hvor mange i din klasse som har taget en rød eller blå T-shirt på i dag. Til venstre på figur 1 kan du se resultatet. Der er 2 som har taget en blå T-shirt på, og 4 som har taget en rød T-shirt på. Der er altså dobbelt så mange, som har røde T-shirts i forhold til blå T-shirts. Du konkluderer derfor, at din klasse går mest i røde T-shirts.
Men hvor sikker kan du være på den konklusion? Kunne resultatet bare skyldes en tilfældighed? Hvis én af personerne i rød T-shirt tilfældigvis havde taget en blå T-shirt på om morgenen i stedet for den røde, ville du være kommet frem til en helt anden konklusion. I det tilfælde ville du havde konkluderet, at røde og blå T-shirts var lige populære. Der er altså stor sandsynlighed for, at resultatet bare var tilfældigt. Resultatet har derfor lav statistisk signifikans.
Eksempel 2
Vi ser nu på et andet eksempel. Du vil stadig gerne undersøge, om din klasse går mest i røde eller blå T-shirts, og du tæller derfor antallet af hver T-shirt igen. I dag er der bare 6, som har taget en blå T-shirt på, og 12 som har taget en rød T-shirt på. Der er igen dobbelt så mange, som har røde T-shirts i forhold til blå T-shirts, og du konkluderer det samme som sidst: Din klasse går mest i røde T-shirts. I dag kan du bare være meget mere sikker på din konklusion. Hvis én af personerne tilfældigvis havde taget en blå T-shirt på i stedet for en rød, ville det ikke påvirke din konklusion særlig meget. Du ville stadig konkludere, at de røde T-shirts var mere populære end de blå T-shirts. Resultatet har derfor høj statistisk signifikans.
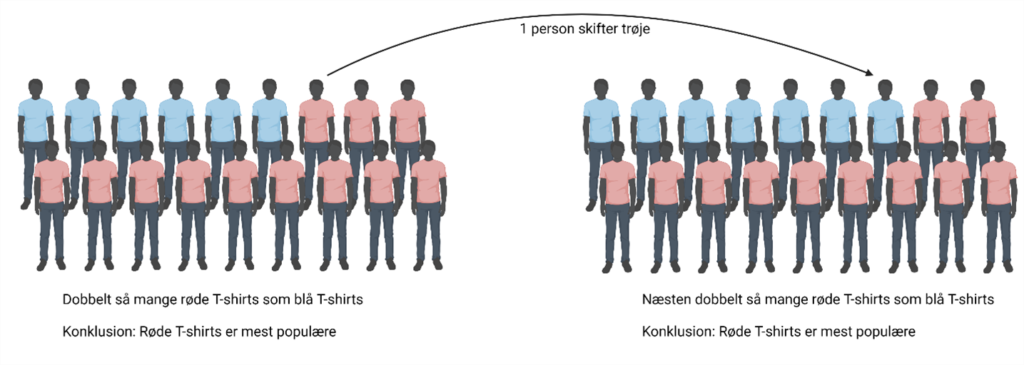
Figur 2: Høj statistisk signifikans. I det andet forsøg er der også dobbelt så mange personer i røde T-shirts som i blå T-shirts. Resultatet af det forsøg er derfor også, at røde T-shirts er mere populære end blå T-shirts. Det resultat er dog mere statistisk signifikant. Hvis én person tilfældigvis havde haft en blå T-shirt på i stedet for en rød, ville det ikke påvirke resultatet særlig meget.
Forskelle i forsøgsresultater kan altså skyldes tilfældig variation, og man kan bruge statistik til at finde ud af, om forskellene er signifikante. Størrelsen på ens datagrundlag – i dette tilfælde hvor mange personer man har inddraget i T-shirt undersøgelsen – har indflydelse på, hvilke resultater man kan kalde for statistisk signifikante.
« Back to Glossary Index
